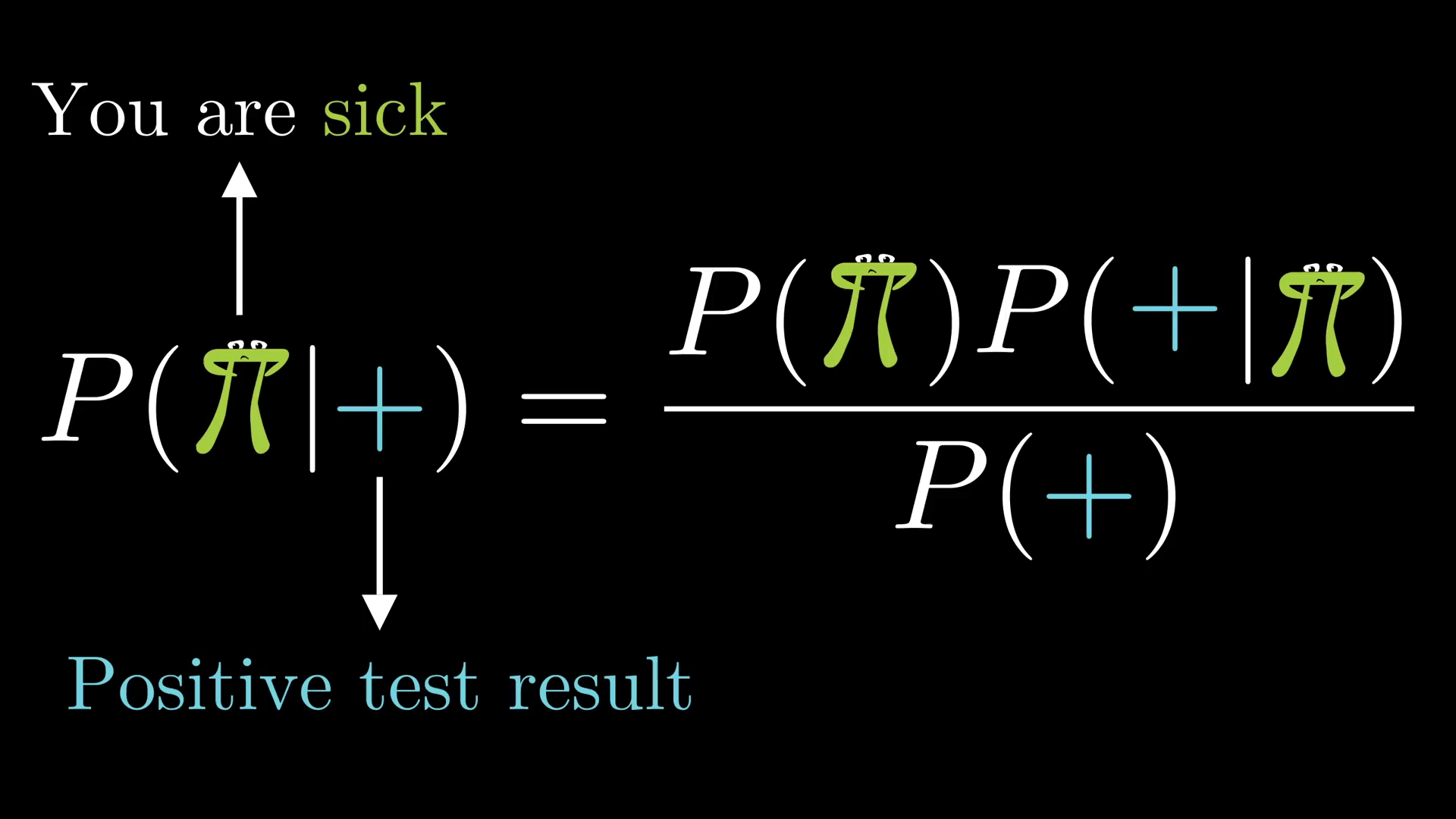本文是观看 3Blue1Brown 的 【贝叶斯定理,使概率论直觉化】视频后所做的笔记,可以算是其“文字版本”。如有问题,欢迎指出。
介绍
陈述
贝叶斯定理(英语:Bayes' theorem)是概率论中的一个定理,描述在已知一些条件下,某事件的发生概率。(维基百科)
公式
P(H|E) = \frac{P(H)·P(E|H)}{P(E)}
其中 P(H) 表示假设(Hypothesis)为真的概率;P(E|H) 表示当假设为真时,看到证据(Evidence)的概率;P(E) 表示看到证据的概率;P(H|E) 表示给定某些证据时假设为真的概率。
理解

它是什么?
知道每个部分是什么意思,然后把具体的数带入计算即可。
为什么是对的?
搞明白它为什么是对的。
什么时候使用?
能够认识到你在什么时候需要用到它。
举例一
描述
来自两位心理学家 Daniel Kahneman 和 Amos Tversky 的研究中的一个例子。
Steve 非常害羞而且性格孤僻,虽然总是乐于助人,但对周围的人或现实世界几乎不感兴趣,他是一个温顺而又井井有条(meek and tidy)的人,需要事情有条理且结构清晰,并乐于钻研细节。
请问“Steve是个图书管理员”和“Steve是个农民”这两种说法哪种可能性更大?
根据 Kahneman 和 Tversky 的实验结果,当人们知道 Steve 是“一个温顺而又井井有条的人”后,大多数人都会说他更有可能是图书馆管理员,毕竟与农民相比,这些特征更符合图书馆管理员的形象。
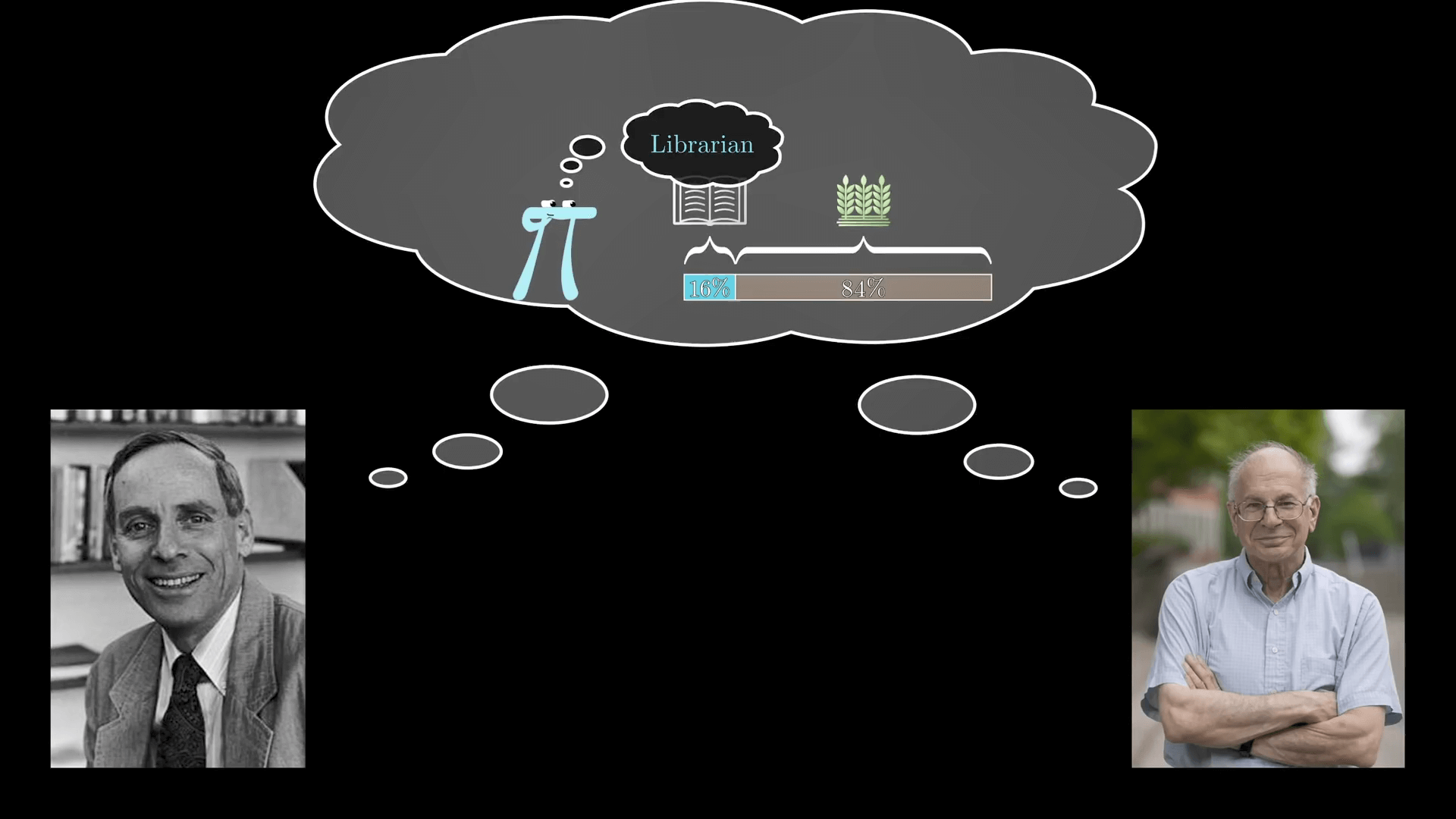
但根据 Kahneman 和 Tversky 的说法,这就是非理性的,为什么呢?
关键问题不在于人们对图书馆管理员和农民的形象认识是否有偏差,而是说在做判断的时候没人把农民和图书馆管理员的比例信息考虑进去。
在他们的论文中,美国农民与图书馆管理员的数量之比是 20:1,实际可能更高,为了方便解释,我们就按 20:1 来算。
事实上我们并不期望所有被问这个问题的人都有准确的关于农民、图书馆管理员以及他们的性格特点的统计信息,但问题是人们是否有考虑过这个比例?从而至少能够做一个粗略估计。
理性不是说知道事实,而是认识到哪些因素是有关的。
如果你真要对这个问题做个估计的话,那么的确有一个十分简单的推理方法。该方法涉及到贝叶斯定理(bayes theorem)背后所有基本推理。
求解
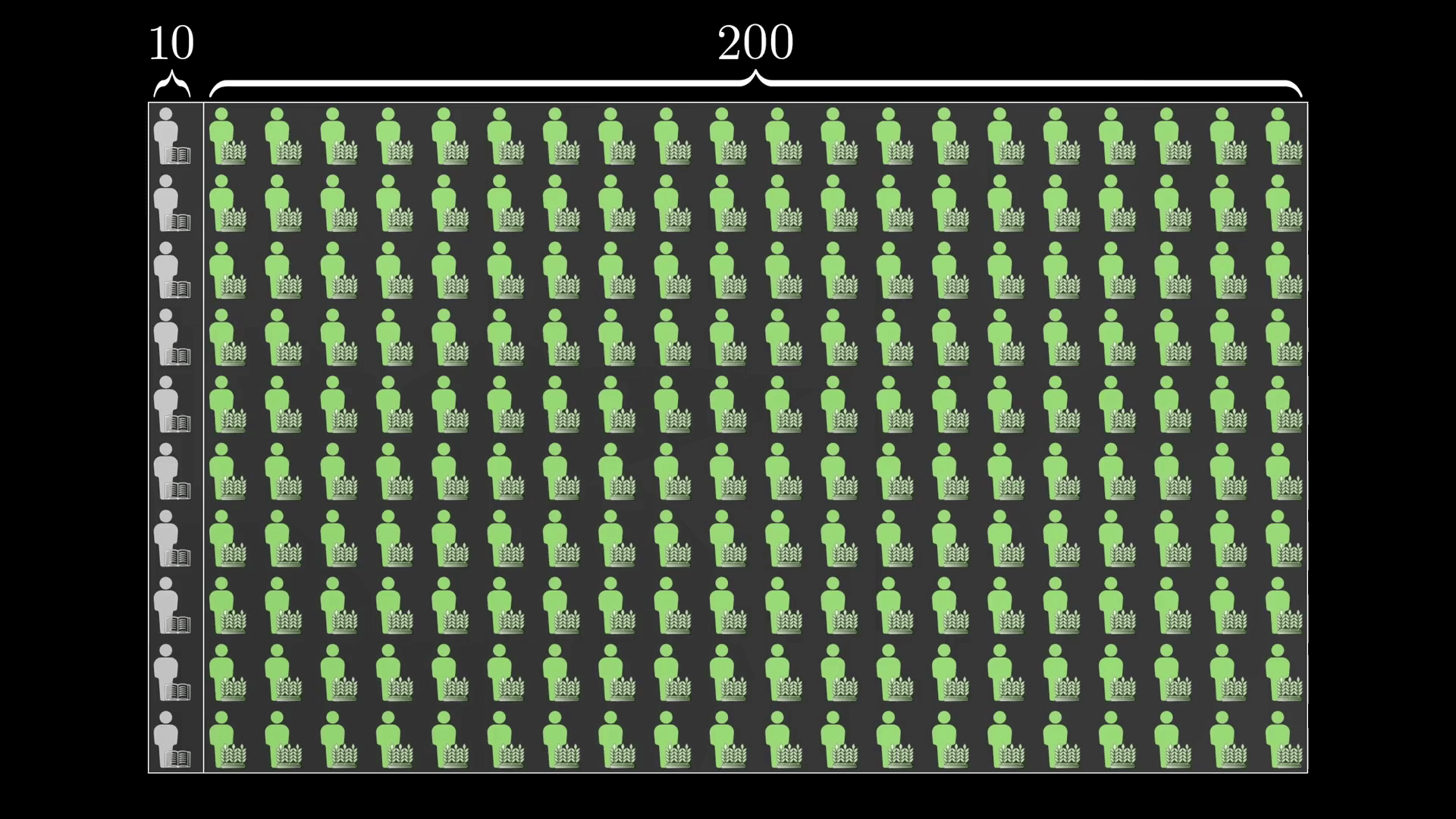
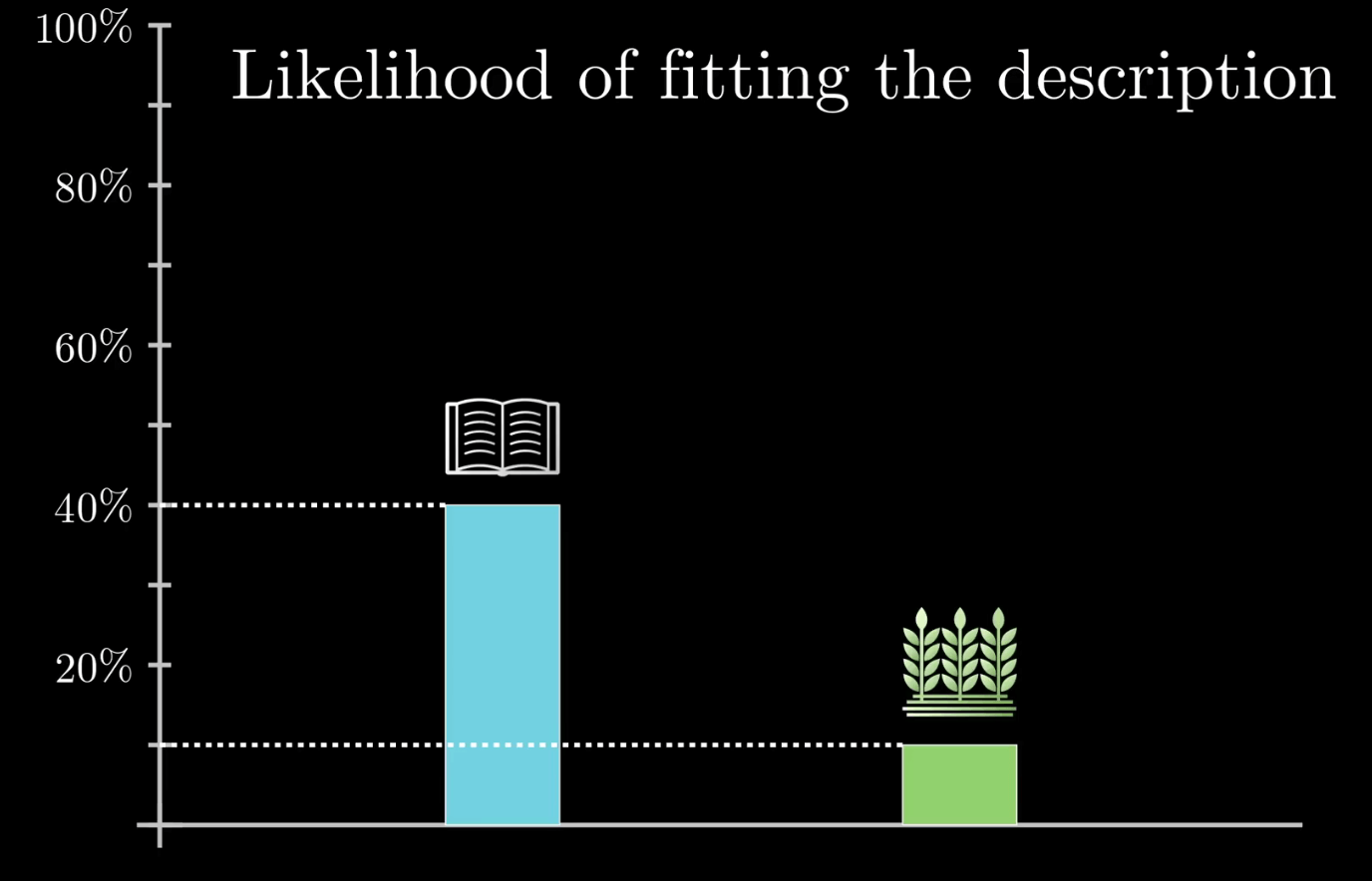
你可以先画个代表农民和图书馆管理员的样本图,比如说 200 个农民和 10 个图书馆管理员,那么当你听到“一个温顺而又井井有条的人”这样一个描述后,我们假定你的直觉是:40% 的图书馆管理员符合这个描述,而只有 10% 的农民符合这个描述。
如果这就是你的估计,那就意味着你的样本中会有大约 4 个图书馆管理员符合这个描述,大约 20 个农民符合这个描述。

所以从满足这个描述的人群中随便抽出一个人,他是图书馆管理员的概率是 4/24 也就是 16.7%。
P(Librarian \ and \ Description) = \frac{4}{4+20} ≈ 16.7\%
因此即使你认为符合这个描述的人是一个图书馆管理员的可能性是是一个农民的 4 倍,也抵不过农民的数量很多。
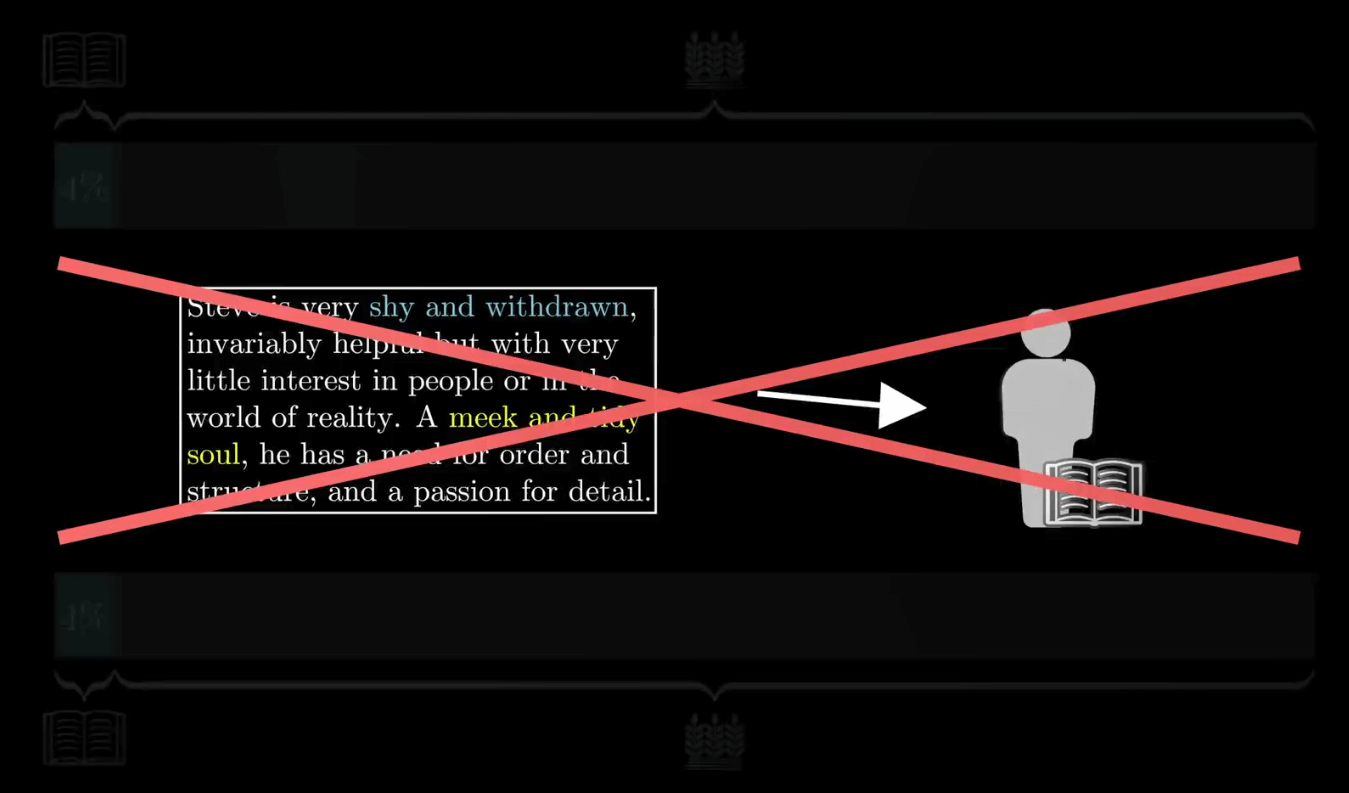
贝叶斯定理最根本的结论也就是说新证据不能直接凭空的决定你的看法,而是应该更新你的先验看法(之前的经验)。

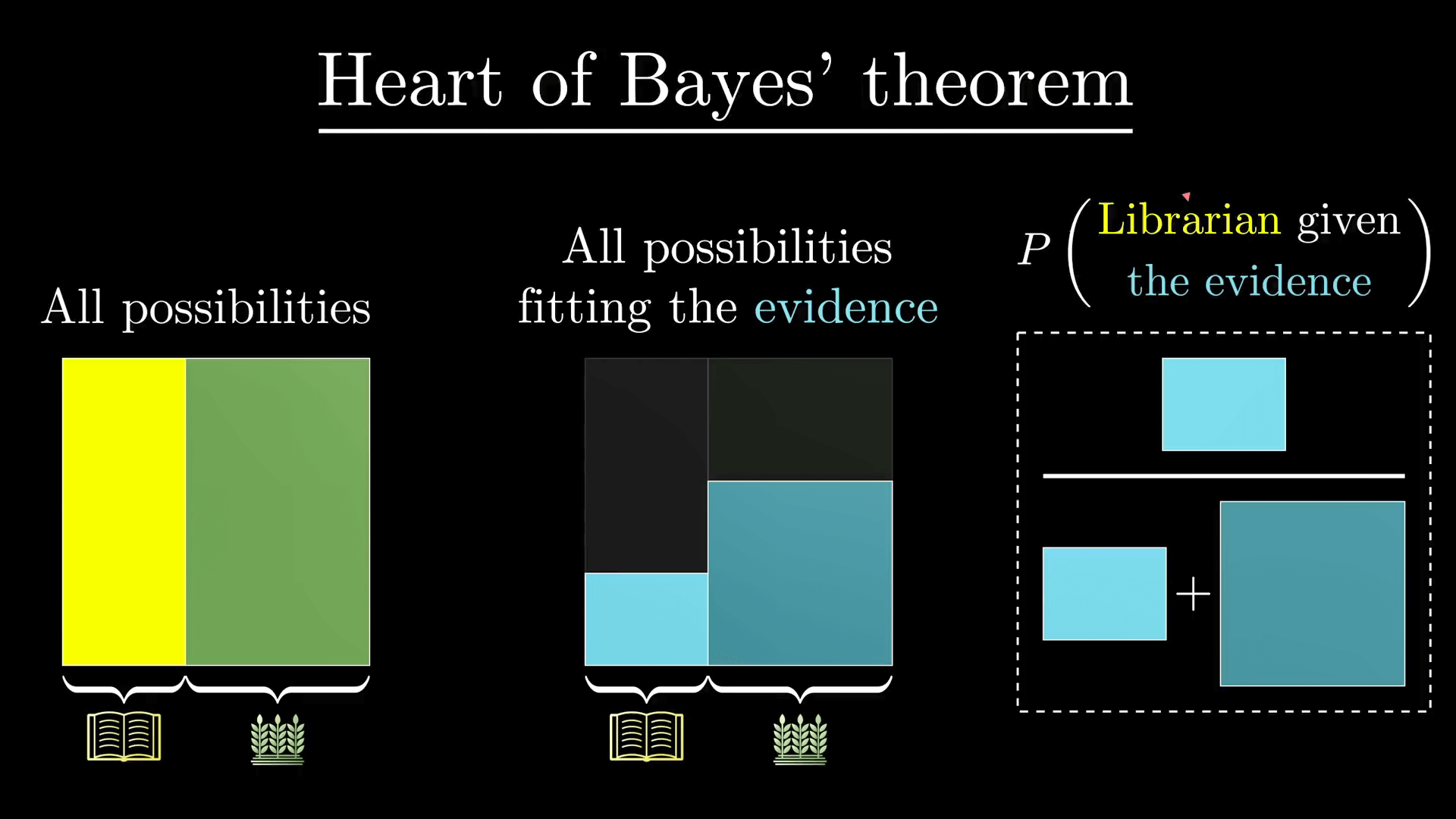
如果你能理解这样的推理,即 看到证据 限制了 概率空间后 再考虑比例,那么恭喜你已经理解了贝叶斯定理的精髓。
或许你要估计的数字各不相同,但重要的是你如何将这些数字组合起来根据证据来更新你的看法。
形式化
理解一个例子只是一回事,我们如何将它写成一个数学公式呢?
与贝叶斯定理相关的更普适的情况是你有一些假设,比如“Steve是个图书管理员”,同时你得到了一些证据,比如口头描述“Steve是个温顺而又并并有条的人”。并且你想知道在“你得到的证据是真的”的条件下“你的假设成立”的概率。
在标准符号中,竖杠 | 表示“在...的条件下”,也就是说我们把我们考虑的情况限制在了证据正确的可能性(条件)下。

回忆我们用到的第一个有关的数字,它是在考虑新证据之前假设成立的可能性,在我们的例子中是 1/21(即 10 / (10 + 200)),它来自于人群中图书馆管理员和农民的比例。这个数字 P(H) 叫做“先验概率”(Prior)。
之后我们要考虑图书馆管理员中符合这个描述的比例——在假设成立的情况下我们看到证据的概率。再强调一遍,当你看到这个竖杠 |,就表明我们只在讨论总概率空间中的一个有限的部分。这里有限的部分就是左侧那一块假设成立(是图书馆管理员)。在贝叶斯定理中,这个值 P(E|H) 也有个特殊的名字,叫做“似然概率”(Likelihood)。
类似的,你需要知道概率空间的另一侧包含多少证据。在假设不成立的情况下我们看到证据的概率,我们使用小拐弯符号 ┐ 来表示“非”。
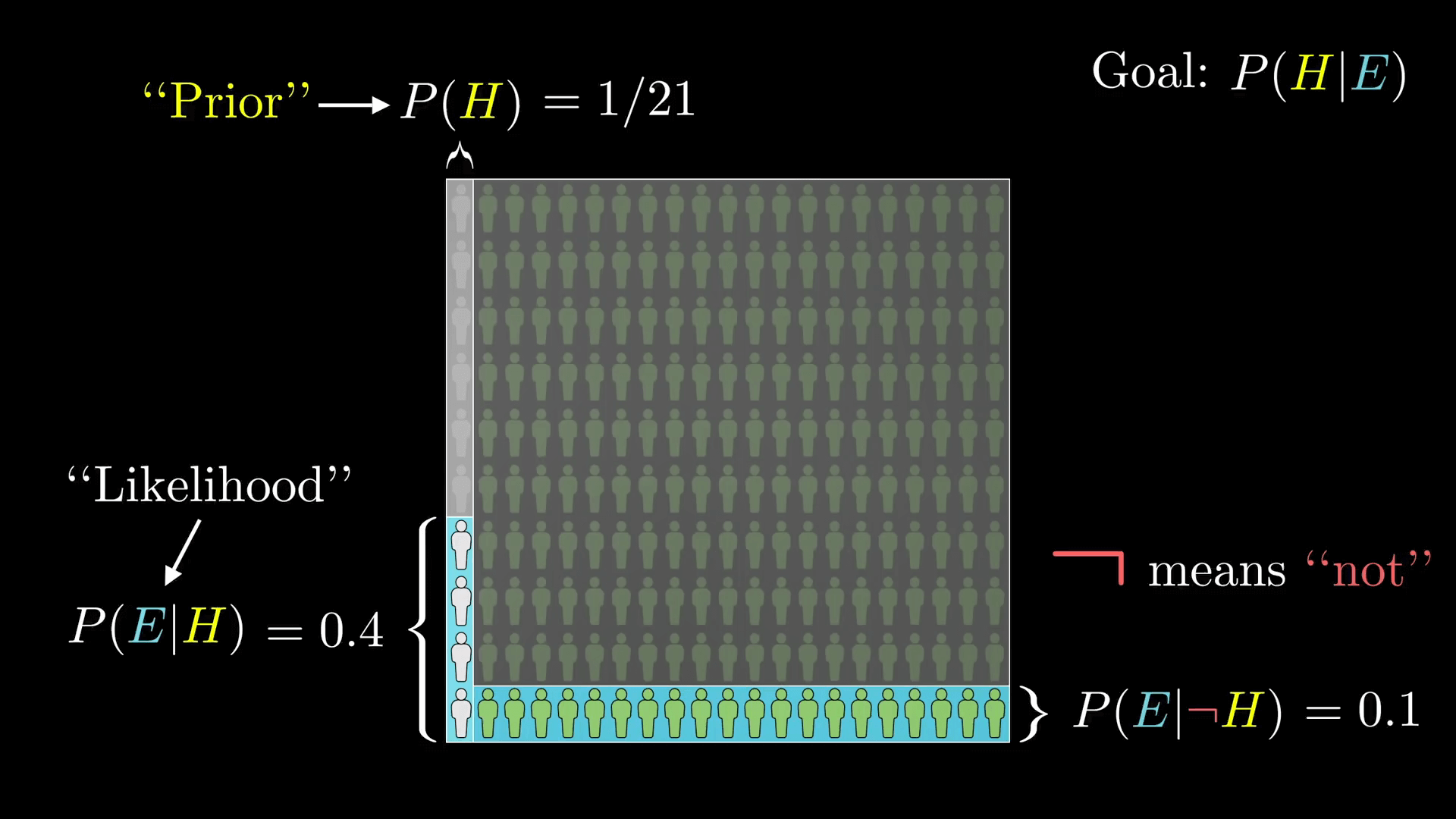
所以有了这些符号后不要忘了我们最终的答案:在证据为真的条件下我们的图书馆管理员假设成立的可能性。也就是所有符合证据的图书馆管理员数“4”除以所有符合证据的人数“24”。
但是“4”是从哪里来的呢?它是总的人数乘以是图书馆管理员的先验概率得到了总共有 10 个图书馆管理员,再用它乘以哪些图书馆管理员中符合证据的概率(即 210*(1/21)*0.4)。
这个数同样也要写在分母上,但我们还需要加上一部分,也就是总的人数乘以不是图书馆管理员的先验概率,再乘以那些不是图书馆管理员中符合证据的比例,也就是 20。(即 210*(10/21)*0.1)。
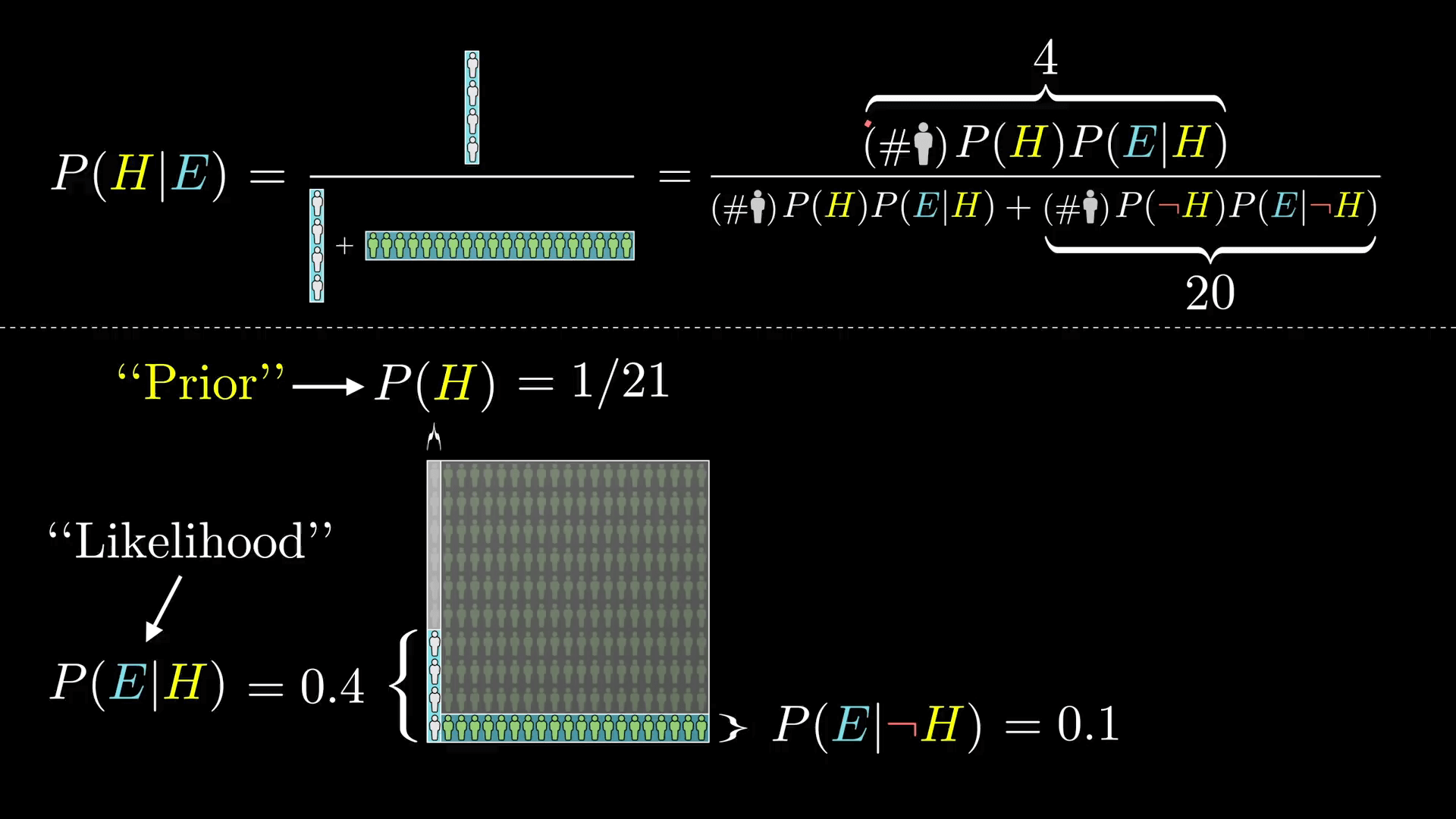
如果我们用 N 表示总人数,那么:
P(H|E) = \frac{N·P(H)P(E|H)}{N·P(H)P(E|H) + N·P(┐H)P(E|┐H)}
注意这里的总人数是可以消掉的,我们最终得到了一个只用概率写出的更抽象的表示:
P(H|E) = \frac{P(H)P(E|H)}{P(H)P(E|H) + P(┐H)P(E|┐H)}
而这个就是贝叶斯定理了,多数情况下,你会看到分母简写成 P(E),即我们在最开始写的:
P(H|E) = \frac{P(H)·P(E|H)}{P(E)}
其中 P(E) 表示看到所有证据的概率,在我们的例子中是 24/210 。但实际上如果你要去算它,你还是需要把它拆成假设成立和假设不成立两部分来算。
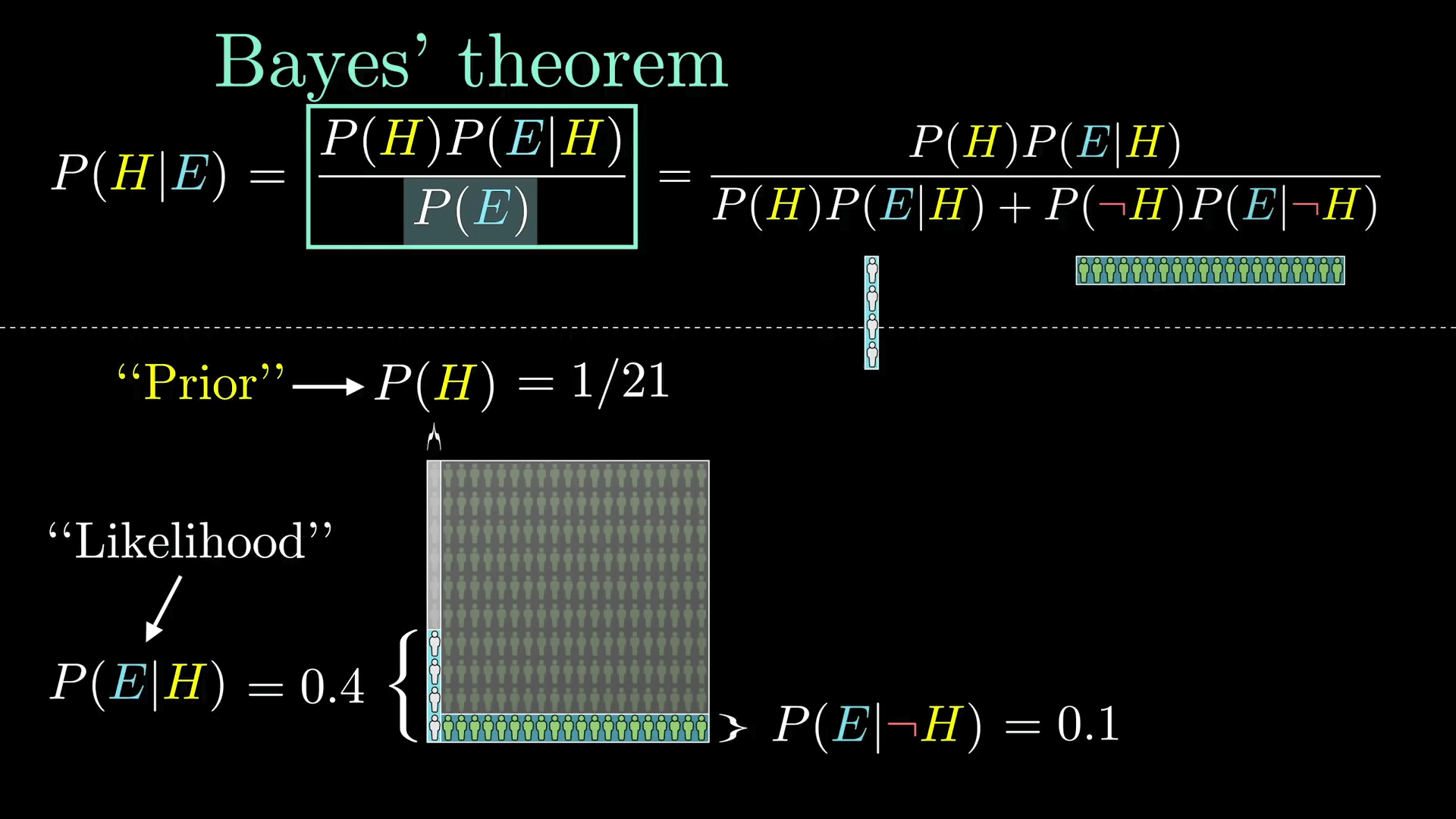
再多补充一点,算出来的最终结果 P(H|E) 叫做“后验概率”(Posterior),也就是当你看到证据后你对假设成立与否的看法。
把它用抽象的公式写出来,看上去或许比直接考虑一个例子的这种代表性样本更加繁琐。不过要知道这样一个公式的的价值在于它能让你量化、系统化的改变你的看法。
科学家会用这个公式去分析新数据到底在多大程度上能验证或否定他们的模型,程序员有时会用它构建人正智能,因为时不时地你会想去显式地数值化地为机器的想法建模。
实话实说,仅从你审视自己和自己观点的方式以及它带给你思想上的改变而言,贝叶斯定理甚至能以某种方式重新塑造你对思想本身的看法。
使用
当例子变得越来越复杂时,使用公式就显得更加重要,事实上你不需要去死记硬背这个公式,而是在你需要的时候就把这个示意图画出来,它是我们例子中代表性样本(representative samples)的一个浓缩提炼版本。
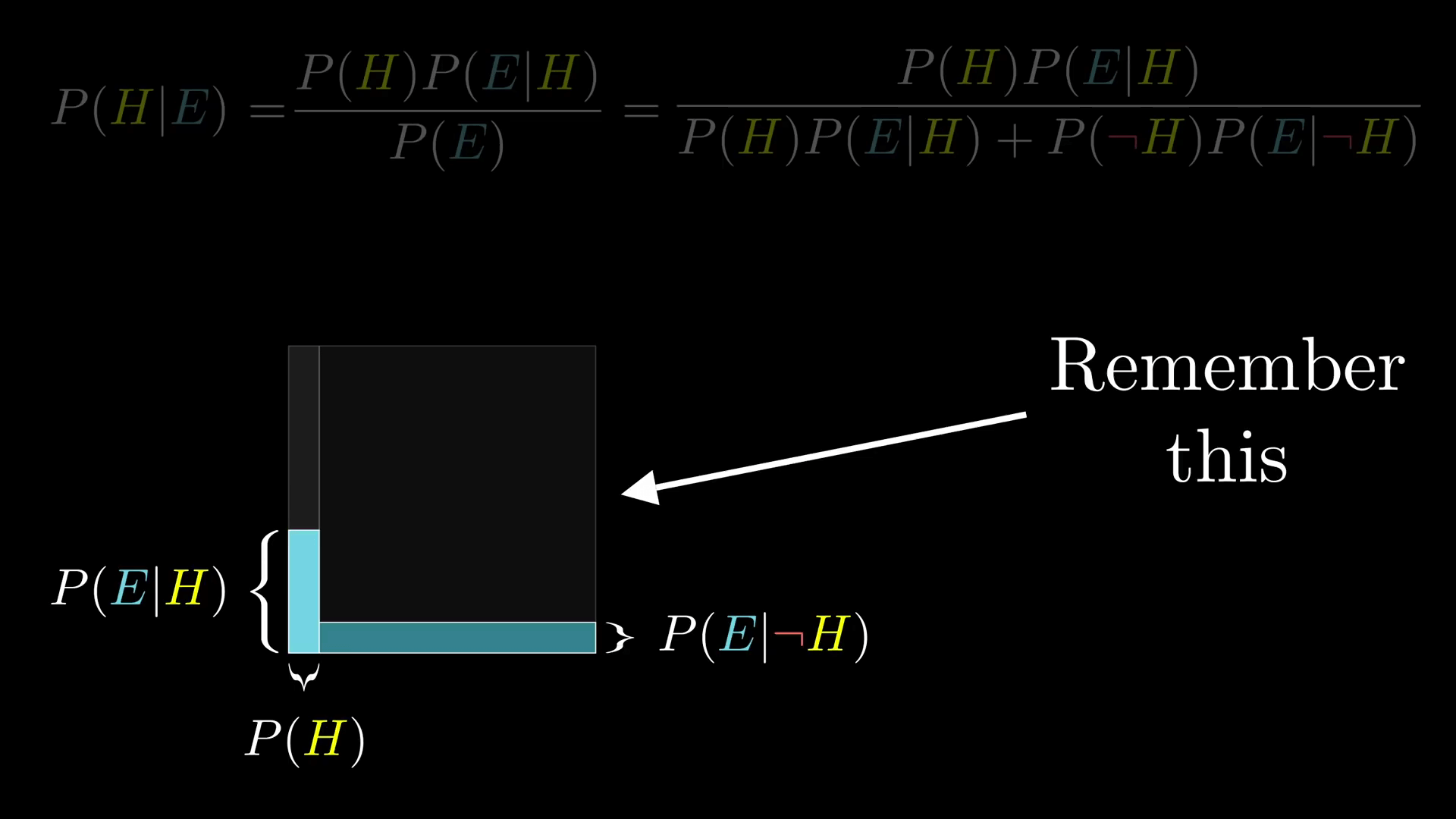
其中我们要考虑的是面积而不是数量,这样更灵活也更容易快速地随时画出来。
不要去想某个特定的数字了,比如 210 什么的。而是把整个概率空间想象成一个 1 * 1 的正方形。之后任何事件都对应概率空间的一个子集,并且事件发生的概率就是子集的面积。
比如,我可以认为我的假设就是正方形的左侧部分,它的宽度是 P(H),不过当我们只看到证据的时候,概率空间就被限制了。而且关键是对左边和对右边的限制程度是不样的。所以在这种情况下假设成立的概率就是它在这个拐弯形状里占据的比例。
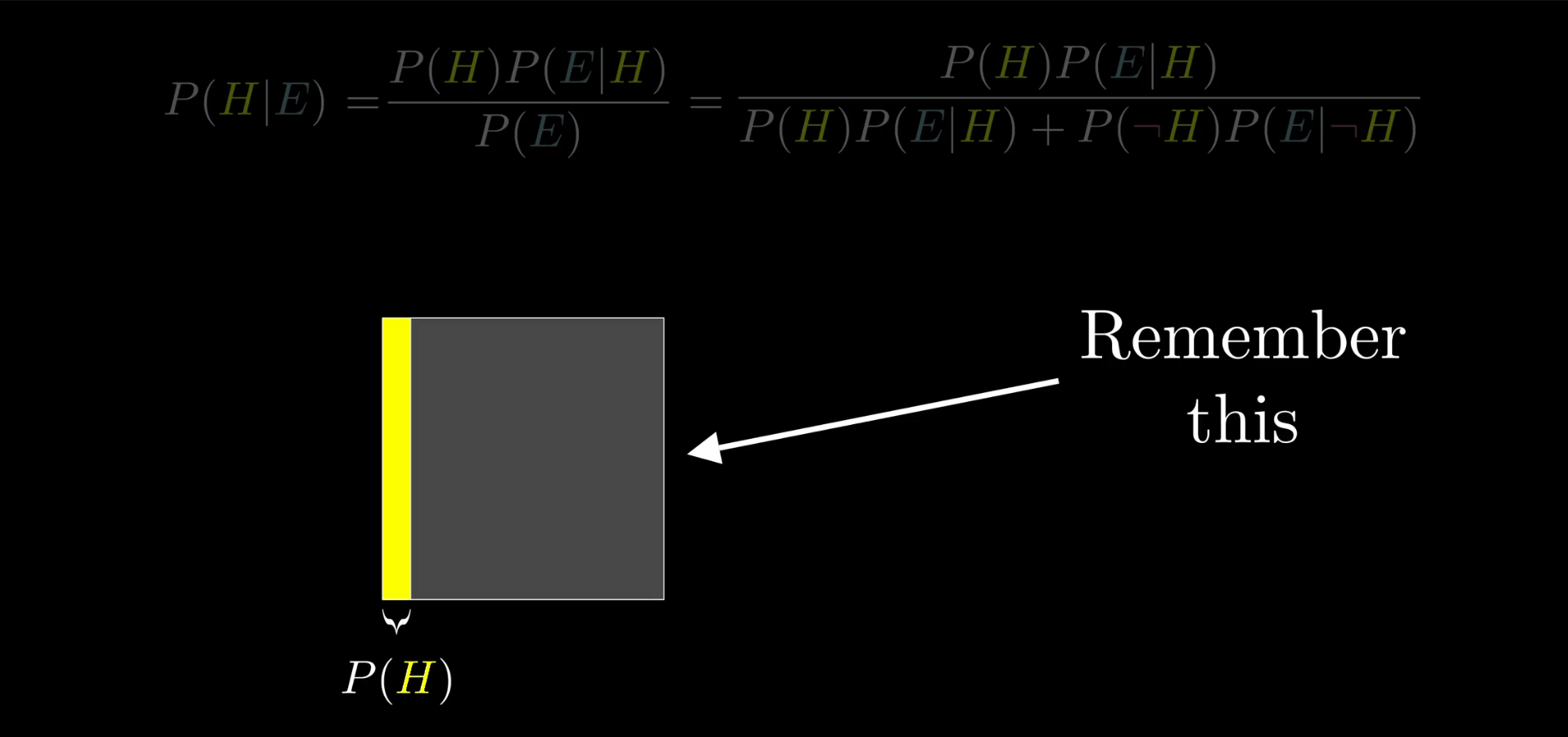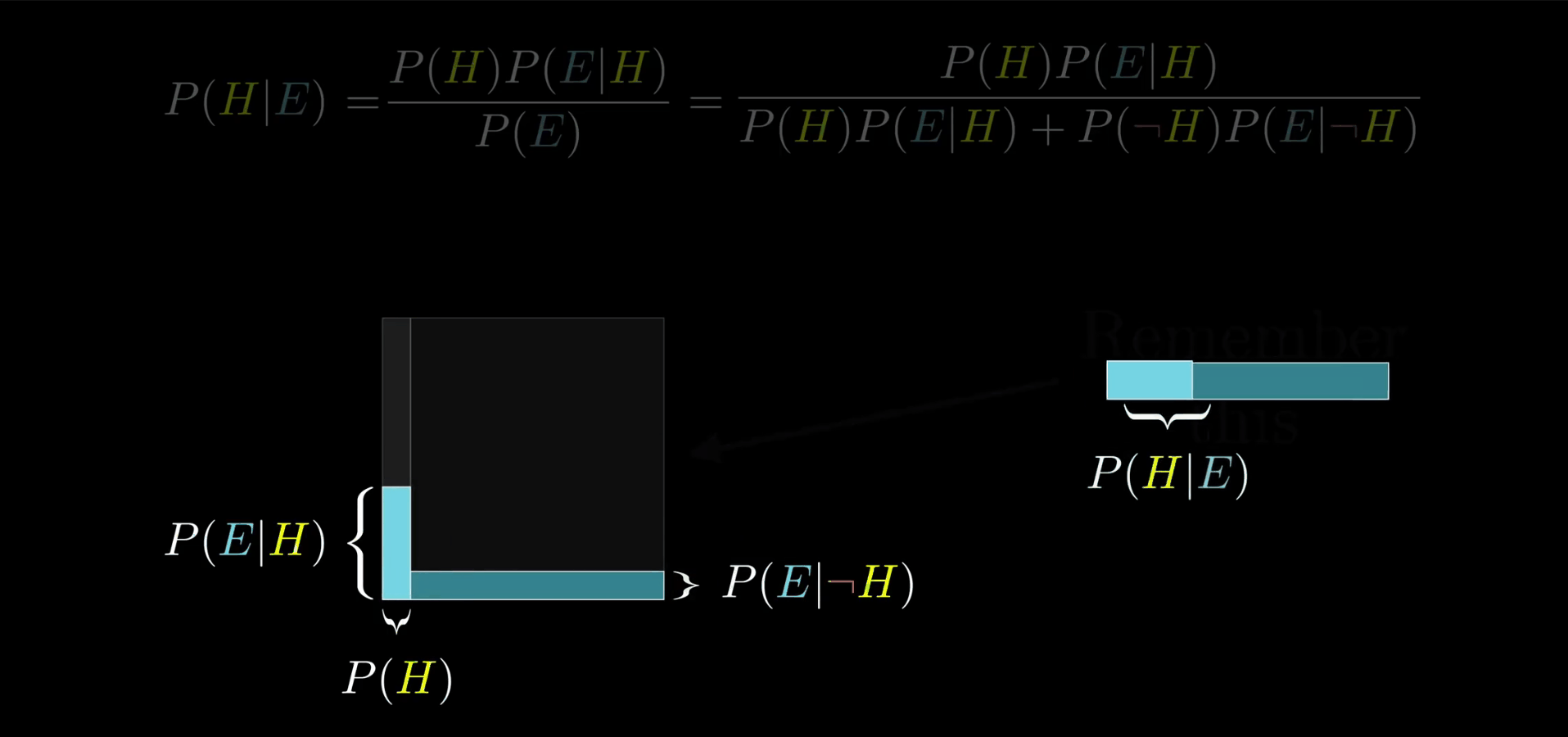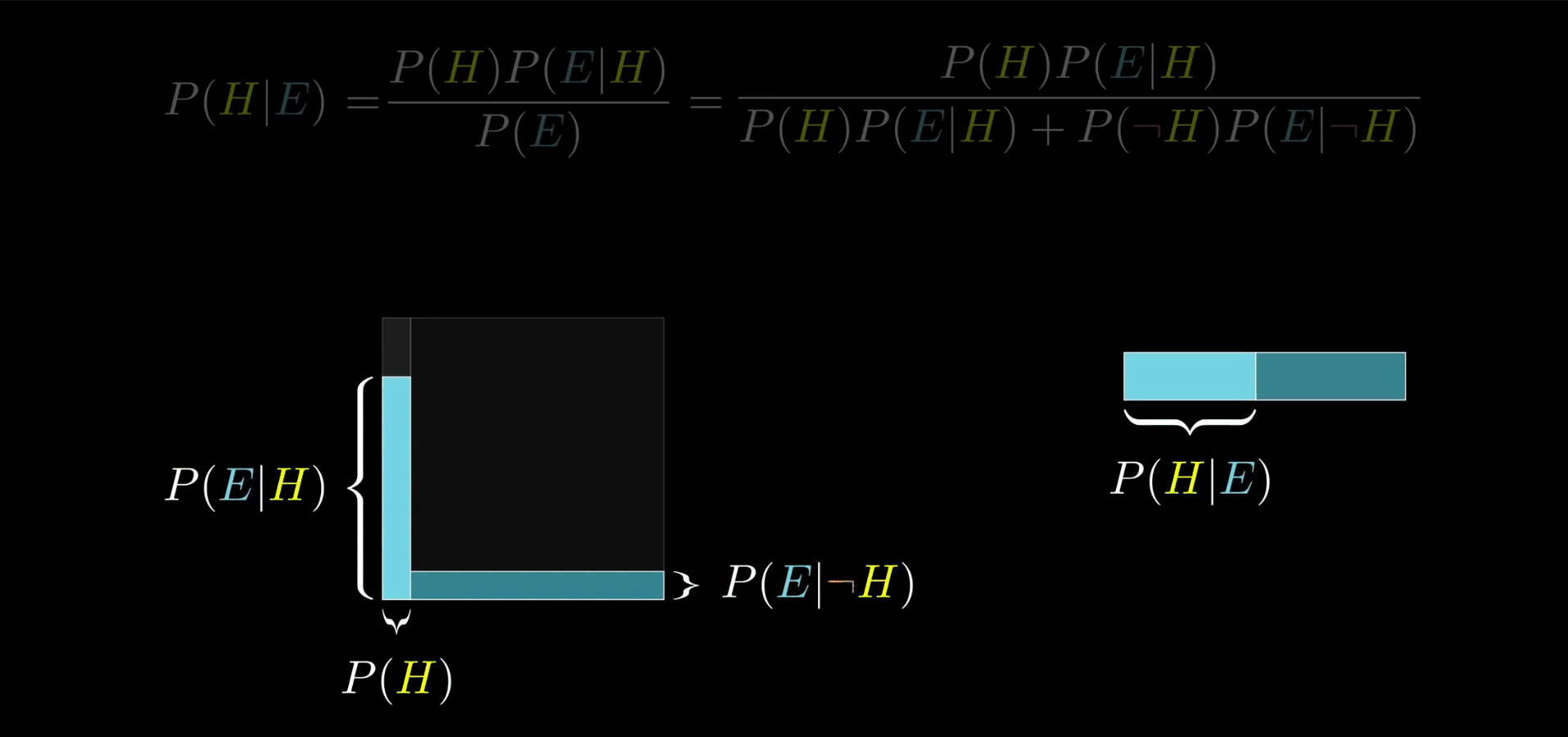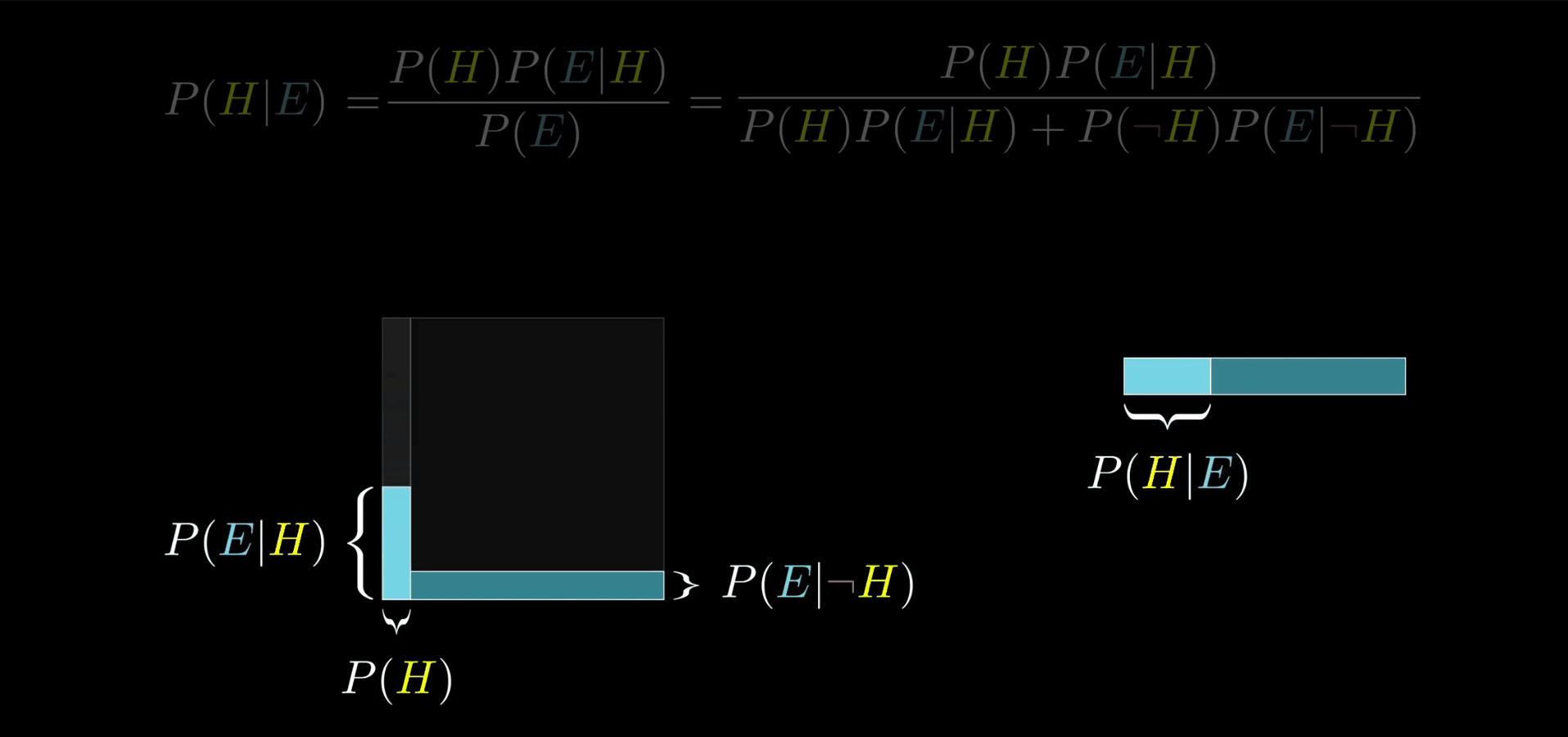
如果你现在突然觉得农民和图书馆管理员等可能地符合证据,那么二者的比例是不会改变的,这应该很好理解,因为无关的证据不会改变你的看法(即 P(E|H)=P(E|┐H),在这里都为 0.4)。

但是如果这些似然概率各不相同,那你最终的看法就会改变很大了。
贝叶斯定理不但说明了这个比例是怎样的,而且如果你想的话你还可以从几何的角度考虑它。比如 P(H)(P(E|H)) 是假设成立同时符合证据的概率,也就是左边矩形的宽度乘以高度,也就是左边矩形的面积。
举例二
描述
其实 Kahneman 和 Tversky 还有一个实验,和 Steve 的那个非常相似。在这个实验中,他俩描述了一个虚构的女人,叫 Linda,Linda 31岁、单身、坦率、而且非常聪明,主修哲学,作为一名学生,她非常关心歧视和社会公平问题,而且还参加反核游行示威活动。
当人们听到这样一个描述后,被问下面哪一种说法更有可能:(1)Linda 是一个银行出纳员;(2)Linda 是一个银行出纳员同时也是女权运动中的一个积极分子。
85% 的参与者说后者更有可能,尽管“是银行出纳员同时也是女权运动中的一个积极分子”是“银行出纳员”的一个子集,前者肯定是比后者少的。
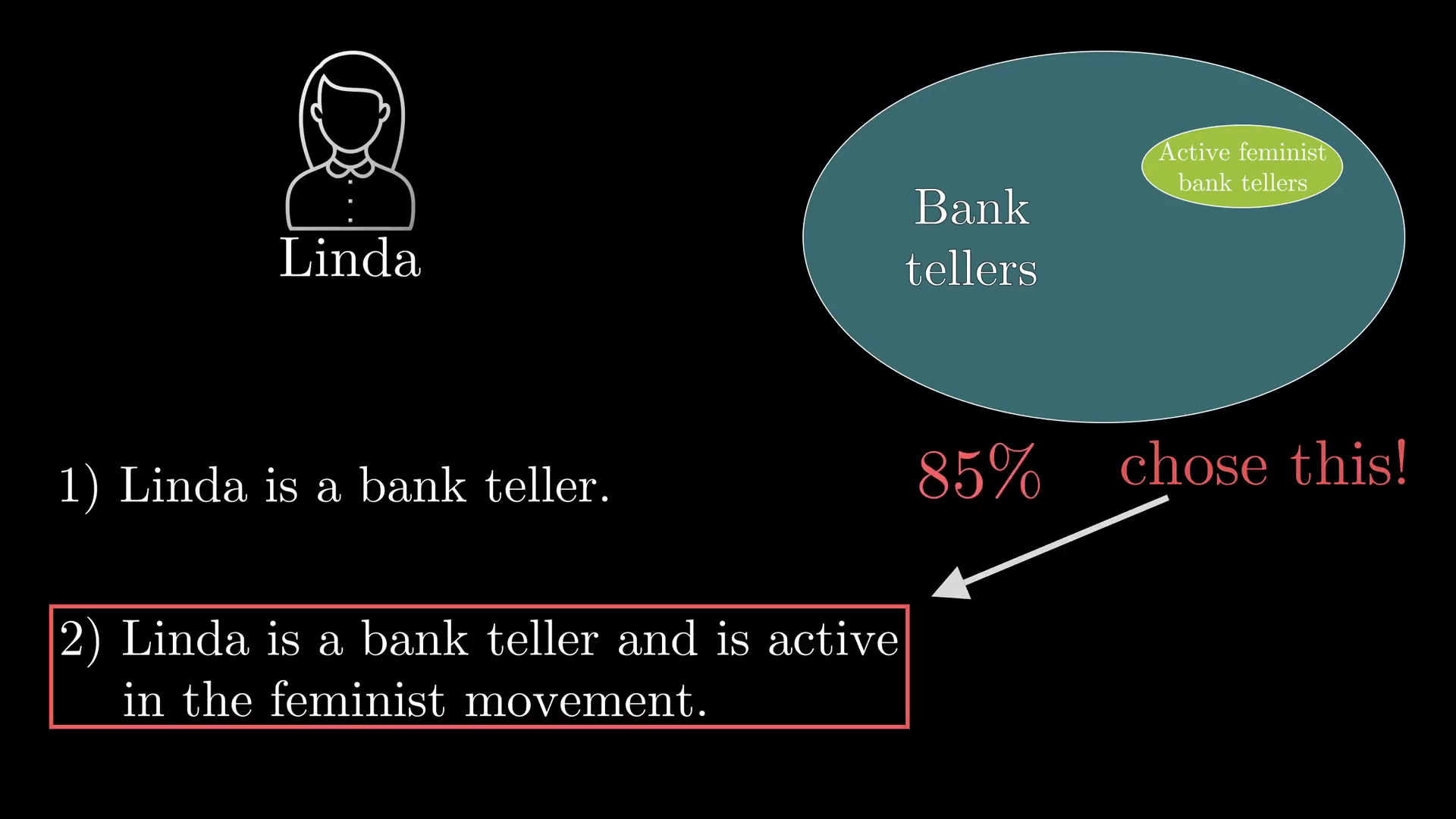
所以出现这种结果的确相当有趣,但更有趣的是,只要我们对这个问题简单地重新组织一下语言,错误率就能从 85% 降到 0。
如果参与者被问说,有 100 个人符合这个描述,(1)其中有多少人是银行出纳员,(2)又有多少人既是银行出纳员同时也是女权运动中的一个积极分子。那么没人会犯错。所有人正确地为第一个选项给定了更高的数字。

思考
奇怪的是为啥像“100个当中有40个”这样一个短语比“40%”能让我们的直觉更准确,而“0.4”这种描述的效果还不如“40%”,效果最不好的是抽象的表达想法如“更有可能”或“更没可能”。
但是又要考虑到代表性样本并不能很好的体现概率的连续性,所以用面积来代替是一个不错的办法,不只因为这个办法体现了连续性,而是说当你拿着笔和纸打算解决一个实际问题的时候,你用这个办法是可以轻松地把草图画出来的。

总结
你也应该认识到了人们认为概率论就是研究“不确定性”,确实,概率论就是这样应用在科学上的。但是概率的数学本质确实就是数学上所说的比例,这些公式也都是由数学比例构成的。在这种情况下,利用几何是非常有助于理解的。
我们把贝叶斯定理当作是一个关于比例的表述,比如人的比例、面积的比例等等。一旦你理解了以后,这种比例的表述就很显然了。
在两个矩形中,你都先只看符合证据的那部分,然后再考虑还满足假设成立的那部分所占的比例,这就是它要表达的意思,公式右边只是告诉你如何计算。

这种直观上关于比例的事实,对科学、人工智能都意义非凡,其实在任何你想要量化你的看法的时候,你都可以用它。
补充
关于 Steve 的例子我们还剩下一点没有说完,有些心理学家在争论 Kahneman 和 Tversky 的"理性的去思考就是要把农民和图书馆管理员的比例考虑进去"这一结论,它们争辩说的理由是背景给定得很模糊:到底谁是 Steve?
他是从所有的美国人中随机抽出来的一个人,还是说他是问你问题的两个心理学家的朋友,或者还有可能是你自己熟悉的一个人。
这些假设都会影响先验概率,比如我在指定的一个月中见到的图书馆管理员远多于农民,而且满足这个描述时是图书馆管理员或农民的概率肯定是高度取决于你如何解读问题。对于我们来说,是为了理解其中的数学
需要强调的是,任何值得讨论的问题,都可以画一个示意图来解决,背景问题改变的是先验概率,而关于性格和印象的问题改变的是其对应的似然概率。
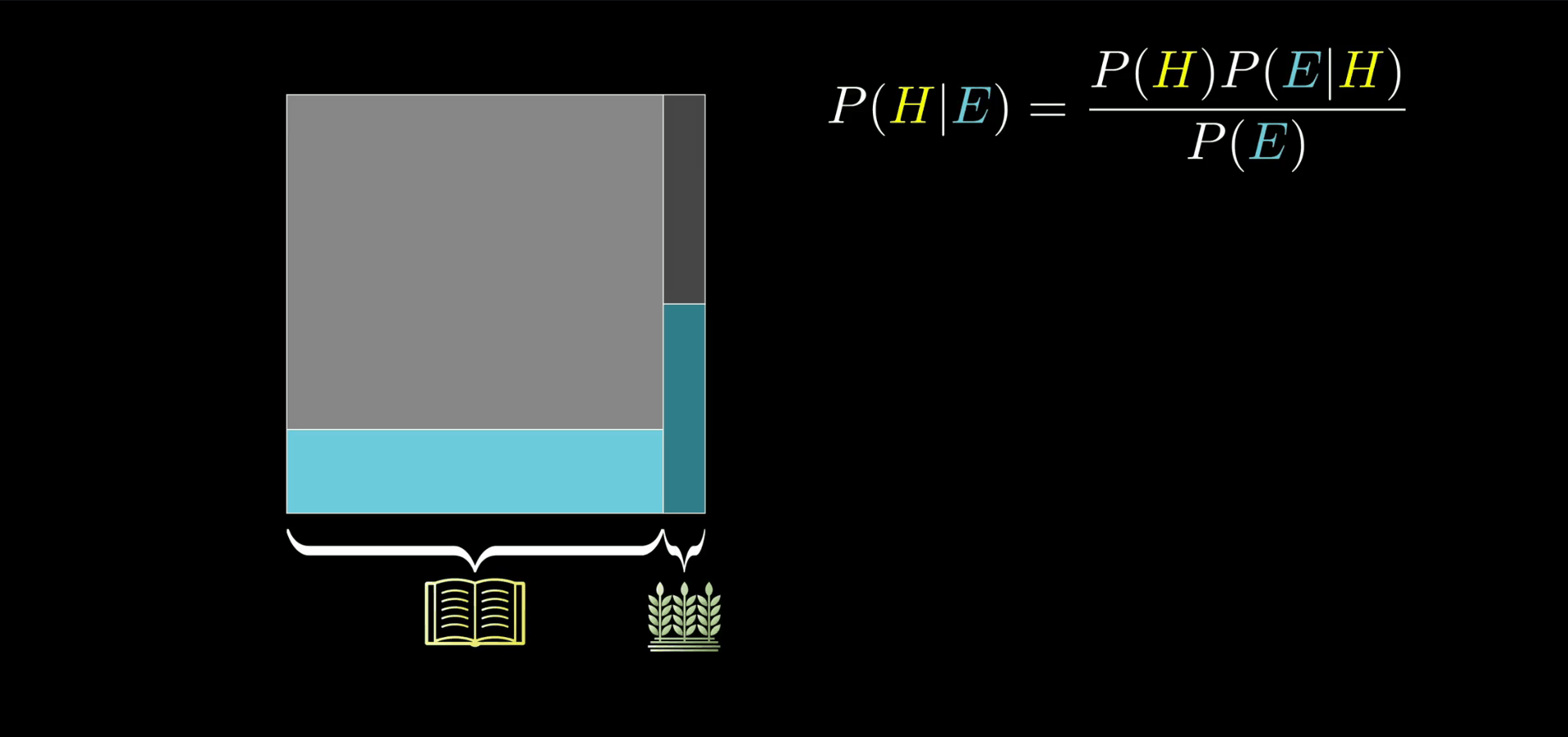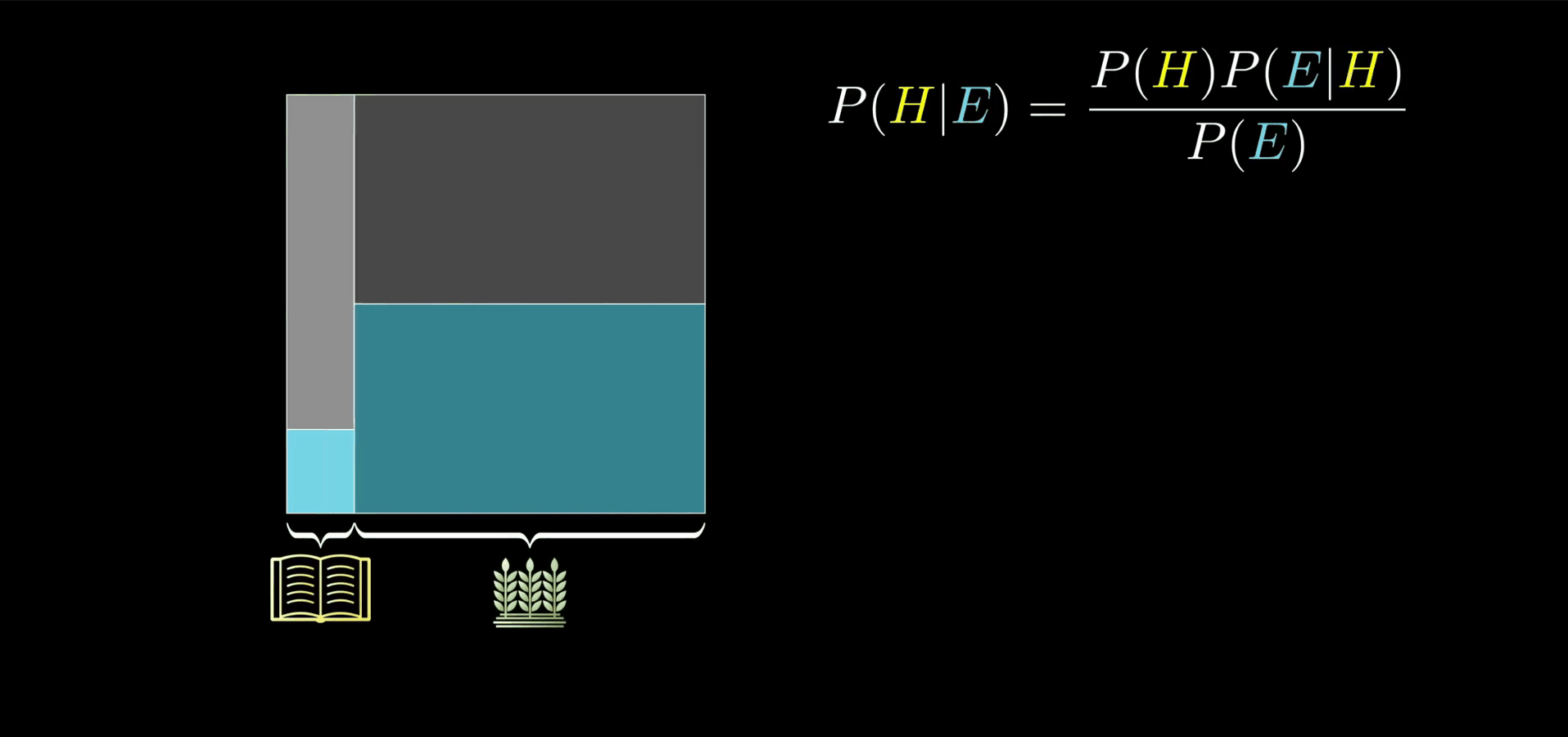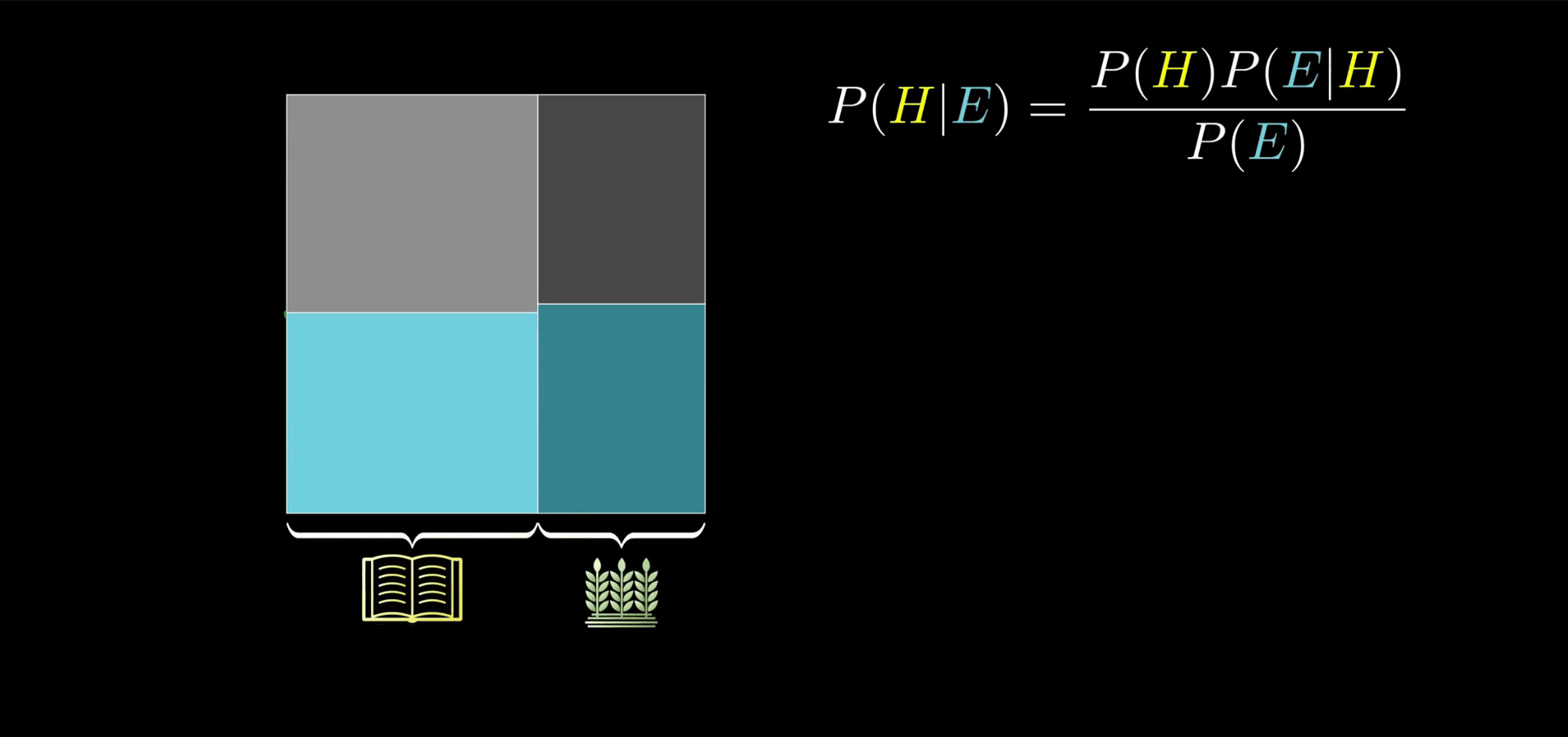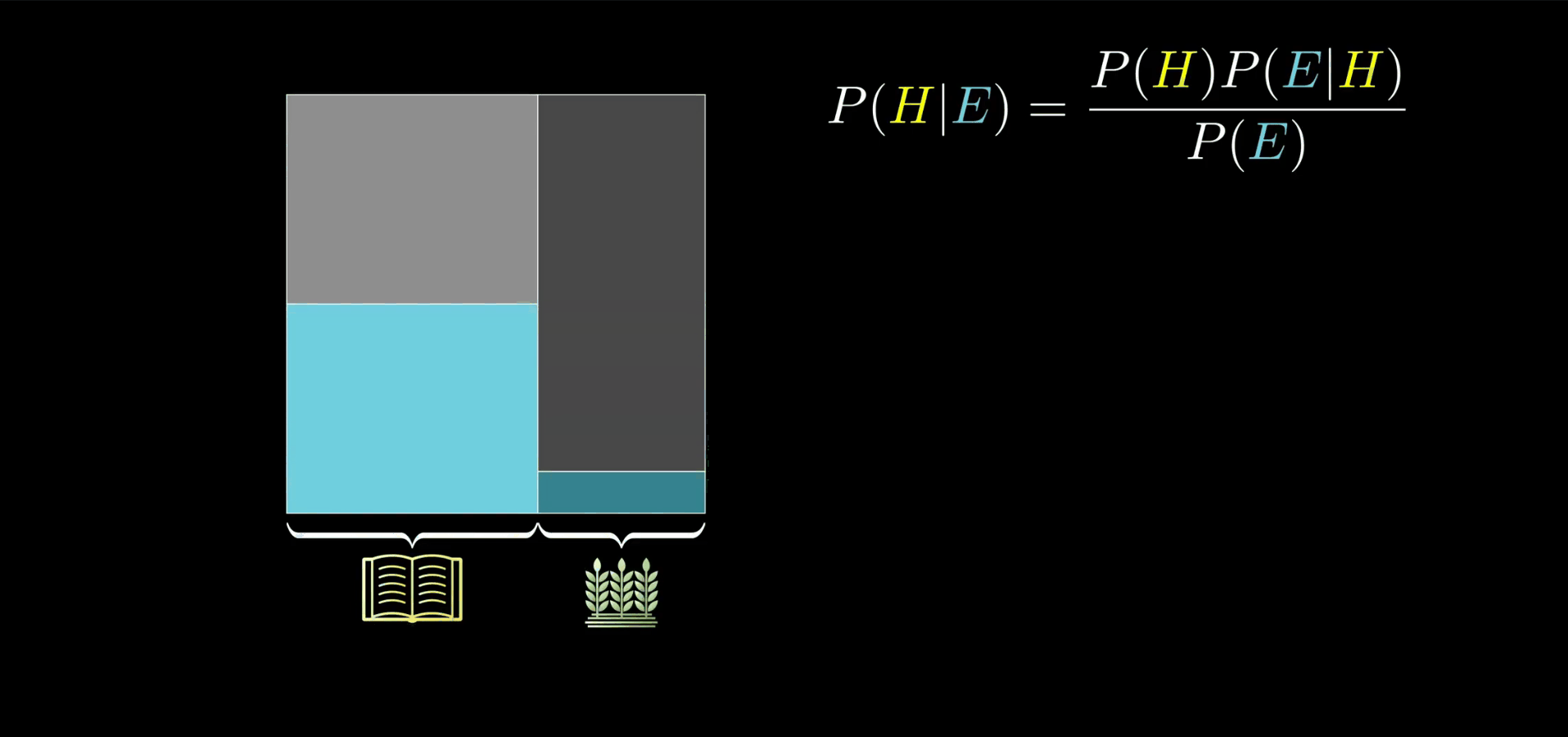
不论你是否认可这个实验,其最终的目的是告诉你:证据并不应直接决定你的看法,而是更新看法。这个思想值得牢记。
没法说这是不是违背了人们的自然本能感觉,这个问题还是留给心理学家吧。更有趣的是,我们应该怎样修正我们的直觉,使它能够真实地反应出数学所蕴含的结果。如果能记住那张图的话,就可以更好的做到这一点了。
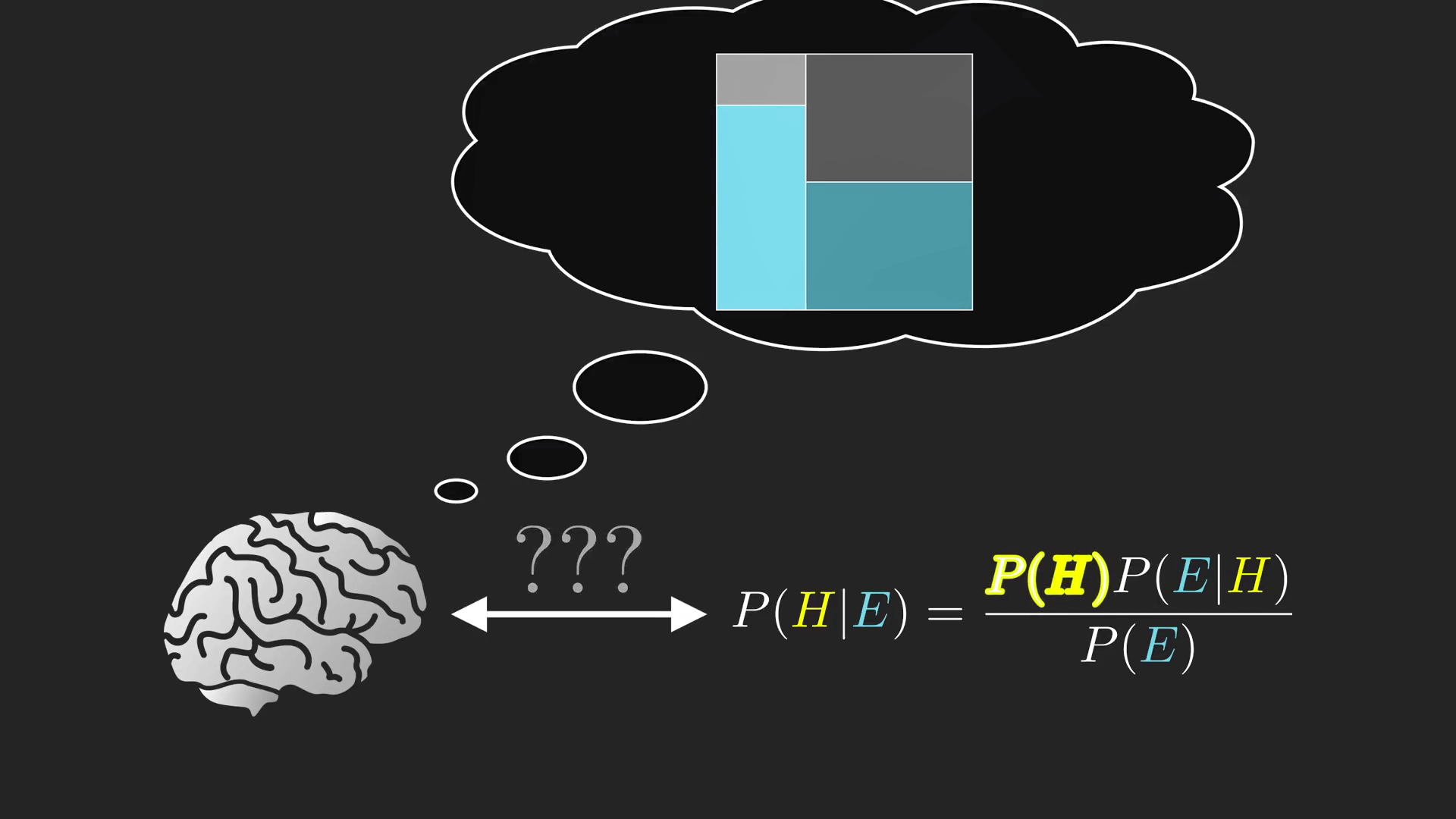
注:想要了解更多数学知识可以关注 3Blue1Brown 的 b 站主页,深入浅出、直观明了地领略数学之美。
推荐
- 刘未鹏 | 数学之美番外篇:平凡而又神奇的贝叶斯方法
- 知乎 | 怎样用非数学语言讲解贝叶斯定理
- 阮一峰 | 贝叶斯推断及其互联网应用(二):过滤垃圾邮件