本文是观看 3Blue1Brown 的 【贝叶斯定理的简洁证明】视频后所做的笔记,以及对某个经典概率问题的解答。如有疑问,欢迎指出。
证明
过程
如果你只想从数学角度简单理解它为什么是对的,那么通过分解“与”这个词在概率论中的作用是一个很快的理解方法。
比如有两个事件 A 和 B ,请问二者同时发生的概率是多少?
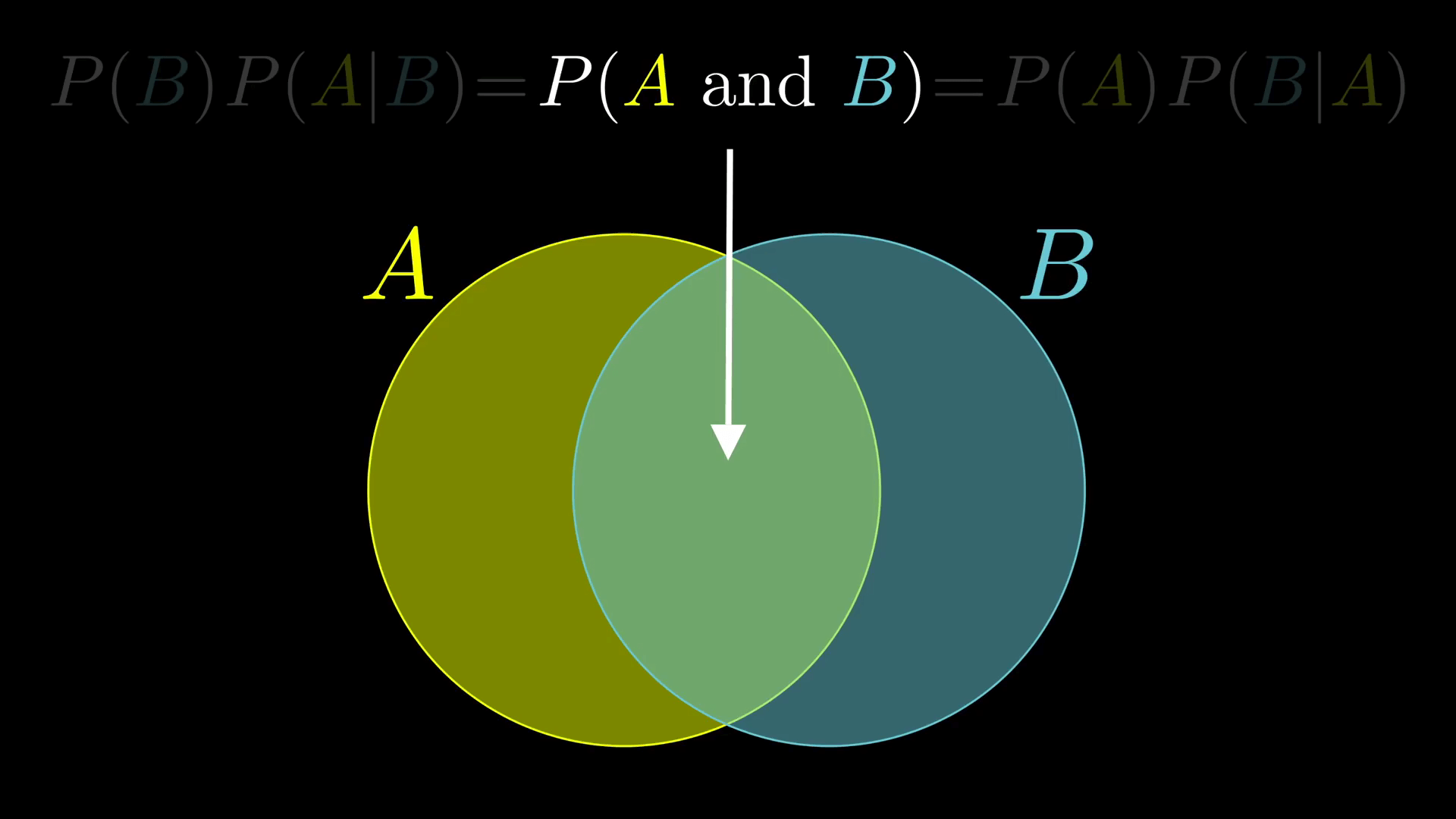
一方面,你可以先写出 A 的概率,也就是所有可能性中 A 为真所占的比例,然后用它乘以那些事件中 B 也为真的比例,也就是在 A 发生的条件下 B 发生的概率。
同样,你可以先写出 B 的概率,然后用它乘以那些事件中 A 也为真的比例。
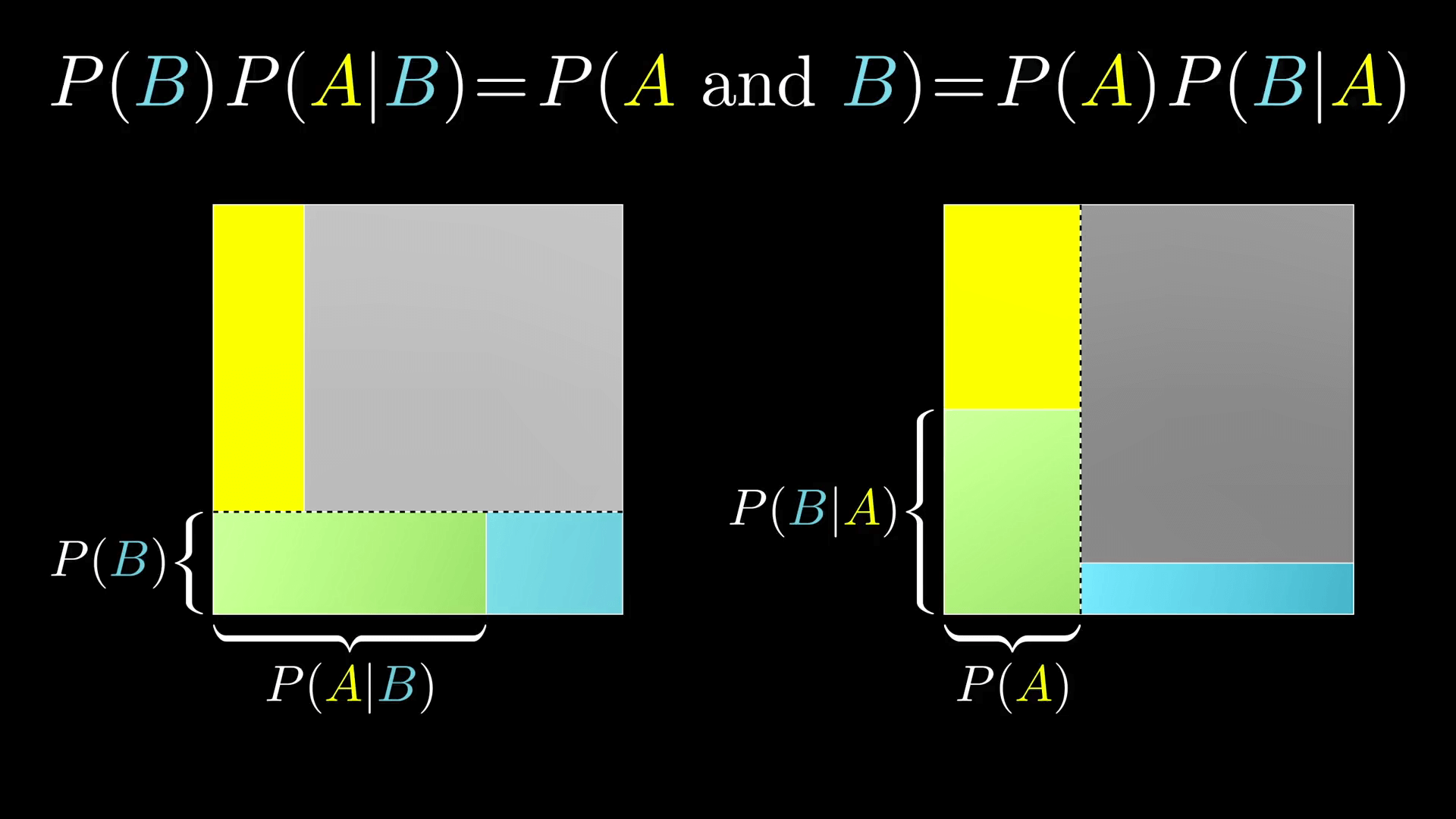
这两种写法是一样的,并且它俩是一样的这个事实给我们提供了一种用 P(B|A) 来表达 P(A|B) 的方法,反过来也一样,如下所示:
P(A \ and \ B) = P(B)P(A|B) = P(A)P(B|A)
P(A|B) = \frac{P(A)P(B|A)}{P(B)}
P(B|A) = \frac{P(B)P(A|B)}{P(A)}
所以当其中一个条件比另一个条件更容易写出时,比如说在给定的假设成立的条件下看到证据的概率比反过来更容易考虑,这个简单的恒等式就变成了一个很有用的工具。
然而,尽管这是一个比较纯粹或者说快速的公式理解方法,但是为了记得“什么时候应该用这个公式”,我们还是尽可能将所有东西都用"证据"和"更新看法"的说法来描述(参看【直观理解贝叶斯定理】)。
补充
此外,还有一个值得强调的常见误解,即 P(A \ and \ B) = P(A)P(B)。
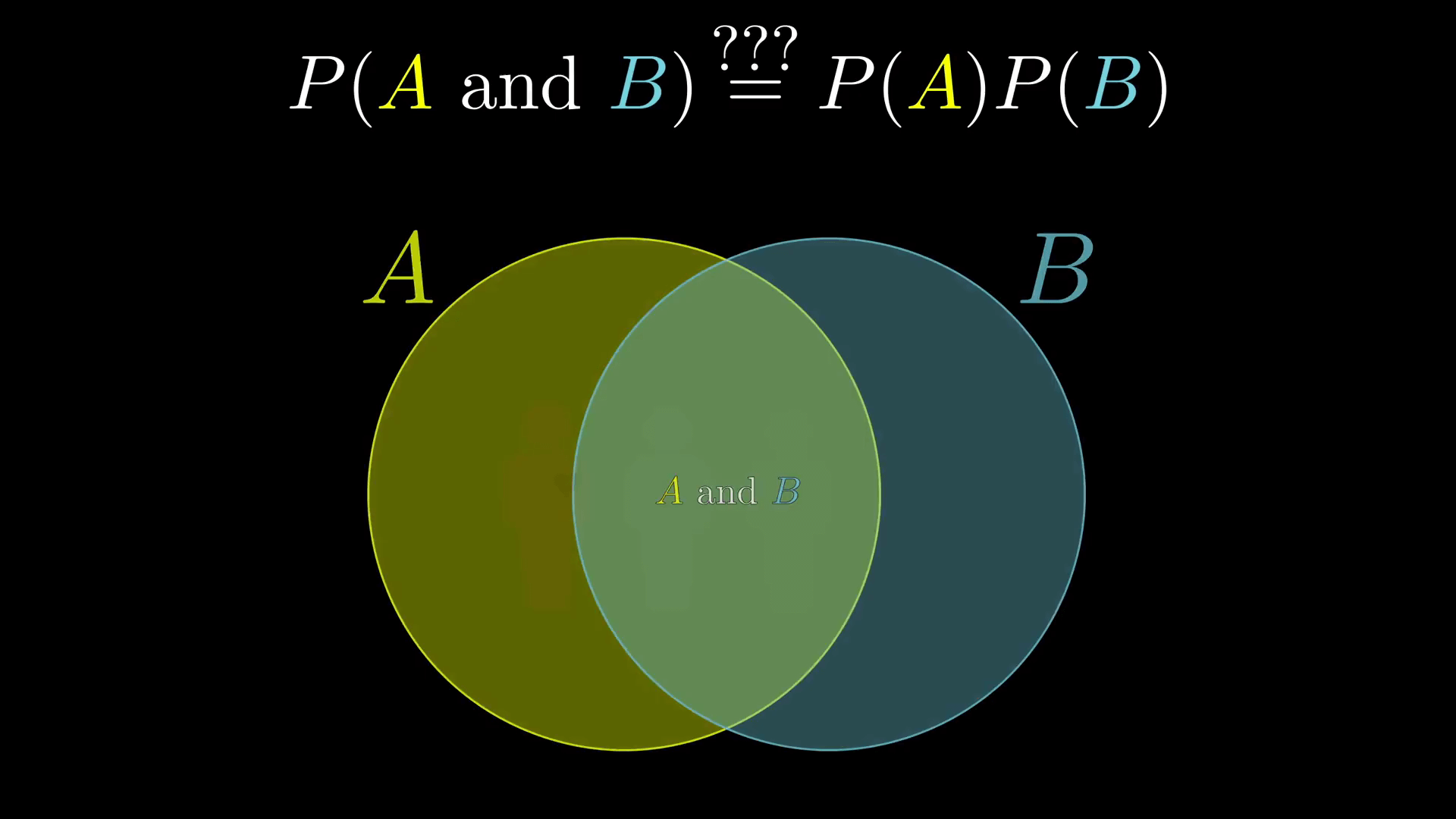
例如,如果你听说 1/4 的人死于心脏病, 那很容易就会去想它的意思是:Steve(无意冒犯,后同) 和他的一个兄弟都死于心脏病的概率是 1/4 x 1/4,也就是 1/16。毕竟掷硬币连续两次反面向上的概率是 1/2 x 1/2,一对骰子掷出两个 1 点的概率是 1/6 x 1/6 。

问题在于相关性,如果 Steve 的一个兄弟死于心脏病,并且考虑特定基因和生活方式的关联所起的作用,那么 Steve 死于类似情况的可能性就会更高些。
这样一个看起来漂亮诱人的公式其实完全是错误的,而像掷硬币和掷骰子这种情况中公式没出毛病是因为每个事件都和它的上一个事件独立,所以 P(B|A) 和 P(B) 其实是一样的,A 事件的发生不影响 B(“独立”的定义)。

要知道许多介绍性的概率例子都是给定在非常游戏化的背景中的,比如骰子和硬币这种都是真正具有独立性的,但所有这些例子都可能歪曲你的直觉。

讽刺的是我们通过这些游戏化的例子想引出的概率论中真正有趣的东西,也即教授这课的初心,只有在非独立事件的条件下才是有意义的。能够精准衡量一个变量多大程度的依赖另一个变量的贝叶斯定理就是它的一个例子。
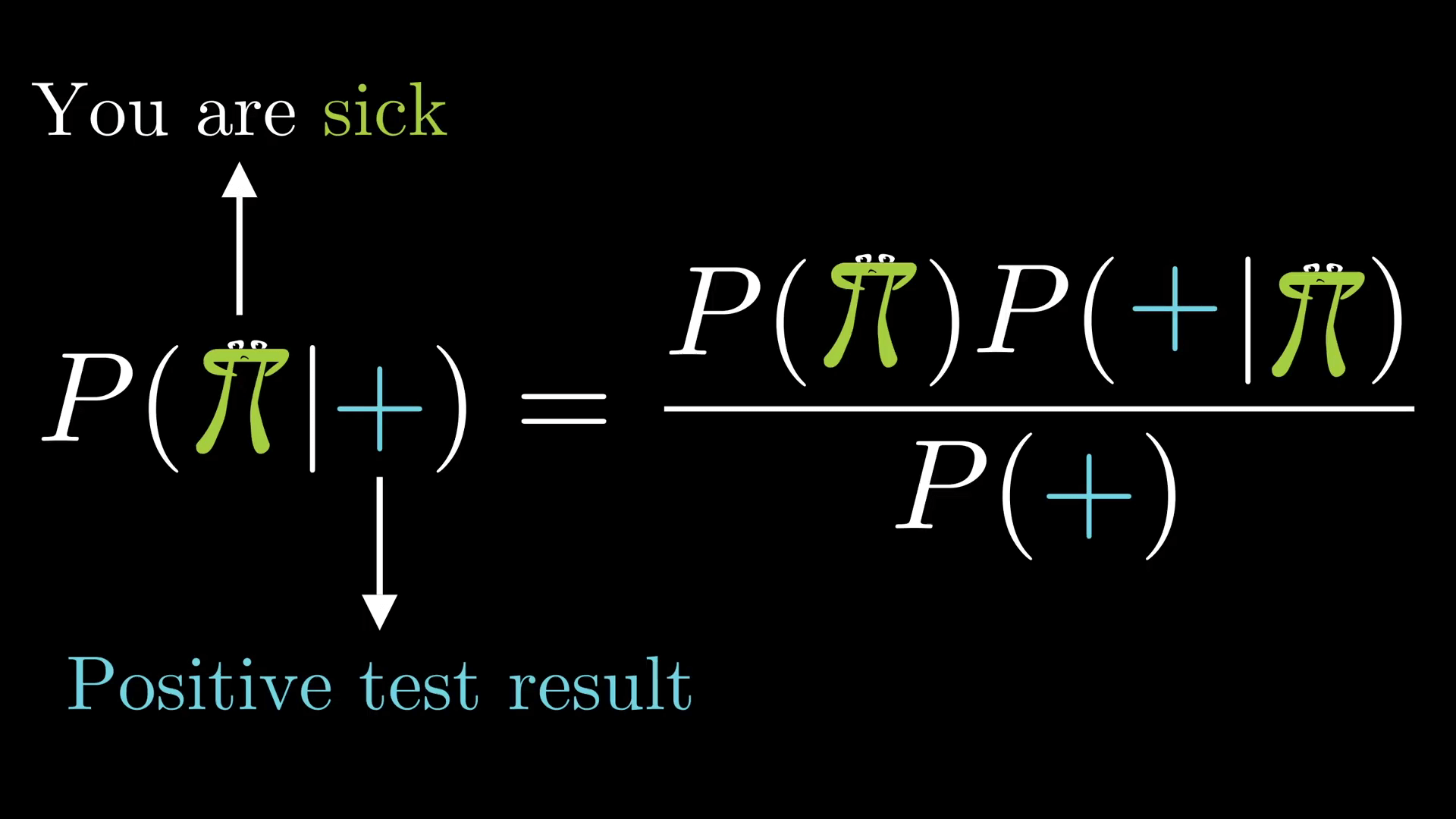
例题
该题来自《批判性思维》书中第 11.6 节的 “体检中的混淆因果”,其实有多个版本,不过核心内容都是一样的。如果你理解了【直观理解贝叶斯定理】中所介绍的贝叶斯定理,并掌握了如何通过图形面积来对相关问题进行求解,那么这个问题就 so esay 了。
描述
Steve(男性)在准确率为 90% 的男性膀胱癌检测中,其检测结果呈阳性,请问这能说明 Steve 有 90% 的概率患膀胱癌么?
或许你会这么想,但需要解释的是,体检呈阳性是针对患有疾病的结果而言的。例如,对男性膀胱癌检测的准确率为 90% ,通常是指,在具备原因的人(膀胱癌患者)中,90% 的人具备结果(体检呈阳性)。
因此为确定 Steve 患膀胱癌的概率,还需要知道另外两方面的信息:(1)多大比例的没患膀胱癌的男性在体检中呈阳性(“假阳性”);(2)男性膀胱癌的发病率(“基准率”)。
求解
我们先定义需要求解的问题:在 Steve 检测结果呈阳性的情况下,请问 Steve 患膀胱癌的概率。那么 P(H|E) 中的 E 代表“检测结果呈阳性”,H 代表“患膀胱癌”。
此外,我们还需要假定:没患膀胱癌的人在体检中呈阳性的比例为 10% ,男性膀胱癌的发病率为 1%。设总人数为 N 为 1000 (其实计算的时候无需使用,这里为了方便作图),如图所示(请忽略面积比例 :)):

使用公式计算的结果为:
P(H|E) = \frac{P(H)P(E|H)}{P(E)} = \frac{0.01 \times 0.9}{0.01 \times 0.9 + 0.99 \times 0.1} ≈ 0.083
因此 Steve 患膀胱癌的概率约为 8.3%,远没有 90% 那么恐怖。

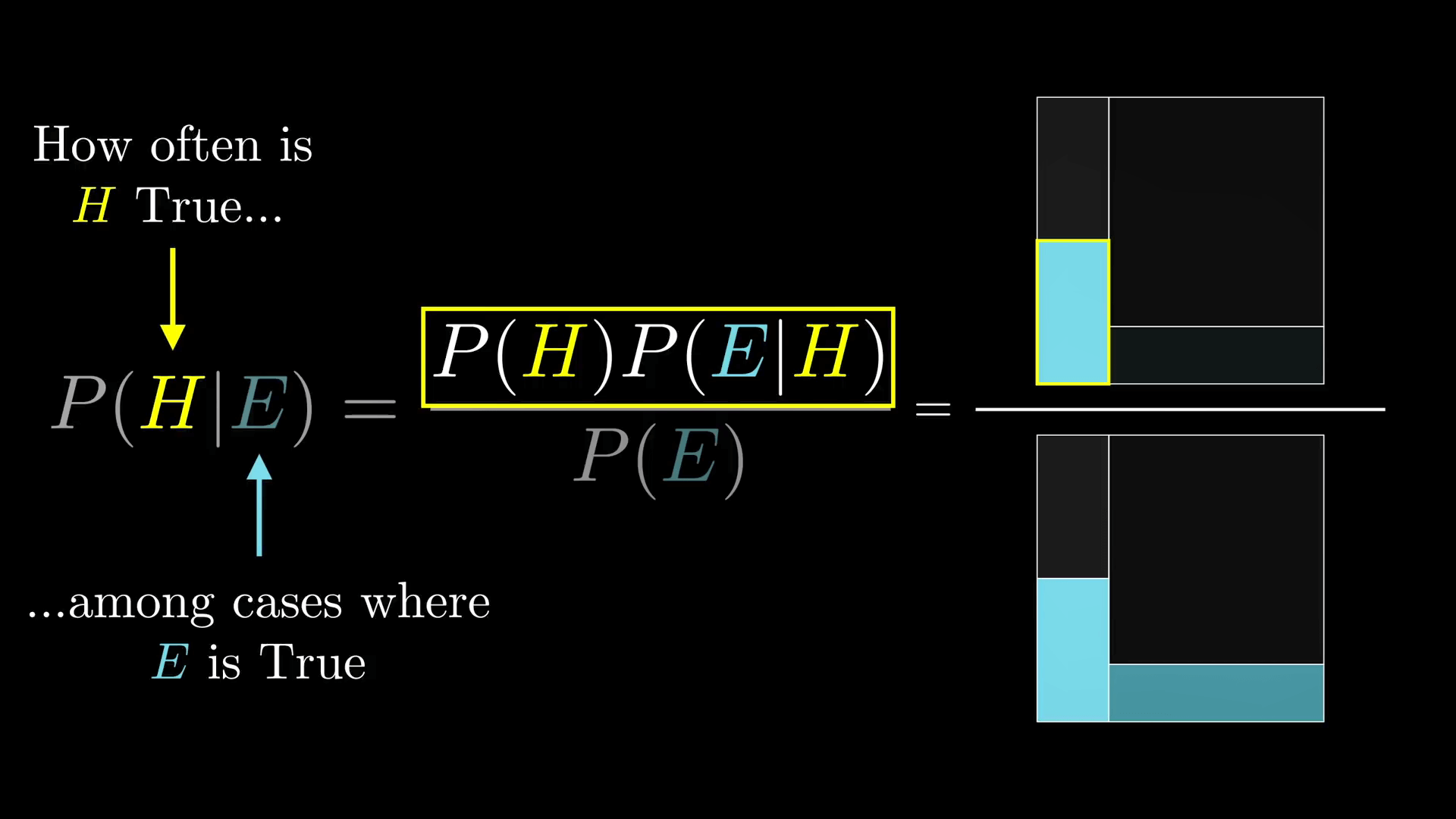
CongTsang
中国上海这集我看过 经典输入法水印,i了i了
经典输入法水印,i了i了